loading...
Teorema Norton untuk menganalisis Rangkaian listrik DC
Norton theorems is that, any two of the series can be converted into an equivalent set of which consists of a current source (IN) and a norton equivalent resistans (RN) with a source flow dipararel it.
Steps to find the rope it is:
1. Specify two of the series who want to search string norton.
2. Determine the amount of the cash flow it is that flows between two terminals in the series who want to search string norton. Because we want to explore the current two terminals must be linked to a series of short first so you can cash flow.
3. Specify the size of the resistans norton is the equivalent resistans review / calculated from the two-terminal series of string which you want to search it. Resistans determine at the time it is, all sources should be eliminated. Voltage source into a series of short relationships and sources of flow into a series of open relationship.
4. Picture a rope to its norton.
Norton theorems is that, any two of the series can be converted into an equivalent set of which consists of a current source (IN) and a norton equivalent resistans (RN) with a source flow dipararel it.
Steps to find the rope it is:
1. Specify two of the series who want to search string norton.
2. Determine the amount of the cash flow it is that flows between two terminals in the series who want to search string norton. Because we want to explore the current two terminals must be linked to a series of short first so you can cash flow.
3. Specify the size of the resistans norton is the equivalent resistans review / calculated from the two-terminal series of string which you want to search it. Resistans determine at the time it is, all sources should be eliminated. Voltage source into a series of short relationships and sources of flow into a series of open relationship.
4. Picture a rope to its norton.
- Example
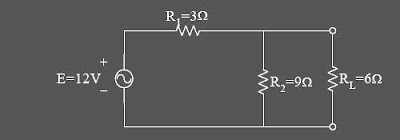
Answer:
To simplify, first series of pictures which you want to rope it is sought, such as the following picture

Determine the flow norton (IN):
relationship short of the first two series of the string it would look for it, so that the circuit is to be:
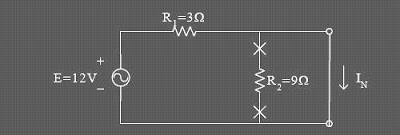
Resistans R2 will not flow because there is a short relationship. Cash will flow through the short series. Norto Flow (IN) then it is, to be:

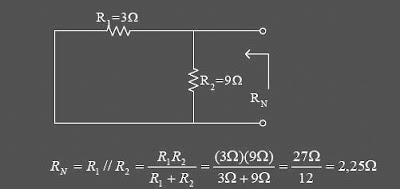
RN specify:
first remove all sources that are in series, so that the voltage source into a series of short relationship (V= 0). Series is to be:
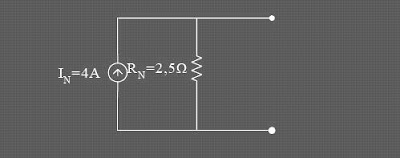
Then combine with the search results Rn and In, of norton String it, can picture the following:
0 Response to "Teorema Norton-Analisis Rangkaian Listrik"
Post a Comment